When first looked upon, a string of binary digits looks quite bizarre and nonsensical. Egyptian hyroglyphics might look more familiar to the unbaptised. Where are the other eight digits? How might one start to make sense of any of this? Why on earth would one choose a numeral system with just two symbols over our beloved and familiar friend with ten: the decimal system? The answers to these questions all lay within the history of early electronic computers and some first-principles of mathematics.
Learning the binary numeral system - or other numeral systems new to us - can be challenging. Usually we are taught binary in the context of computer science, rather than pure mathematics, and usually quite a bit later on in our journey of mathematics and computers. We are taught the Hindu-Arabic decimal system from as early as we can comprehend numbers and we never look back. From then on those ten digits are our best friends and with them we explore the rest of that which the world of mathematics has to offer. Years later we come across the shocking revelation that other numeral systems exist: we must now unmarry the decimal system from the first principles of mathematics we have ingrained in the folds of our minds - we’ve been duped! However, all is not lost, and the key to understanding binary has been with us all along - ever since we learned to count past ten!
Decimal | Base 10
Before we look at binary, let us take the decimal numeral system and place it under a microscope to see what’s going on. This should be easy - perhaps even tedious - as we’ve been using this system all our lives! Firstly, let’s look at what unique symbols we have to play with within this system.
'Zero' 0
'One' 1 *
'Two' 2 * *
'Three' 3 * * *
'Four' 4 * * * *
'Five' 5 * * * * *
'Six' 6 * * * * * *
'Seven' 7 * * * * * * *
'Eight' 8 * * * * * * * *
'Nine' 9 * * * * * * * * *
As you can see we have ten unique symbols at our disposal. Each with a name which is only important in the domain of language which, really, we’re not interested in, but is given here as another example of how we tend to communicate numbers. Each value we’ve listed here also comes with a neat little symbol or glyph we can use to easily represent it. Finally, and most importantly, each symbol carries its own semantic meaning about how many things it symbolises, or to put it in a manner more succinct: each symbol conveys a unique cardinality. This cardinality is completely abstract without context. Luckily, as humans we are quite good at dealing with the abstract.
Because the magic number in this case is 10, we can also call the decimal system base 10. “Base 10” basically means that this system has a total of ten symbols with which we can uniquely represent every cardinality from zero up to but excluding 10. Now that we are well-acquainted with the members of the decimal system, what can we do with them? It would be quite useless if we could only represent ten different numbers with them. The decimal system is a positional base 10 numeral system, which means that we can string together multiple digits to express large numbers, with the position of each digit denoting a different factor of the numeral system’s base - in this case 10. For the sake of keeping the scope of this article reasonable, we’ll only be concerning ourselves with positional numeral systems.
Now, let’s take the number 42 for example. Using just two symbols from our system we can express a much larger number than either symbol alone. How have we done this? This question might seem trivial and unecessary, but taking the time to answer it will allow us to understand more than just the decimal system. We start by looking at the right-most - or the least significant - digit: 2. As this digit is zero digits from the right, we multiply it by the 0th power of our number system’s base (10):
2 * 10^0 =
2 * 1 =
2
So we end up with 2. So far so good, if not painfully trivial. Let’s move on to the next-least-significant digit; 4, which is also the most significant digit as it is the left-most digit and zero places from the left. We are one digit in from the right now, and so we multiply the digit in question by the 1st power of 10:
4 * 10^1 =
4 * 10 =
40
And now we have 40! The last step is to sum up each value that each digit has given us:
40 + 2 =
42
And there we have it. We can now conclude that 42 in decimal is equal to … 42 in decimal. Not very exciting, I’m afraid. However, what we have actually discovered is a formulaic way of calculating the value of any number represented in a numeral system of any base. Here is that formula in all its glory:
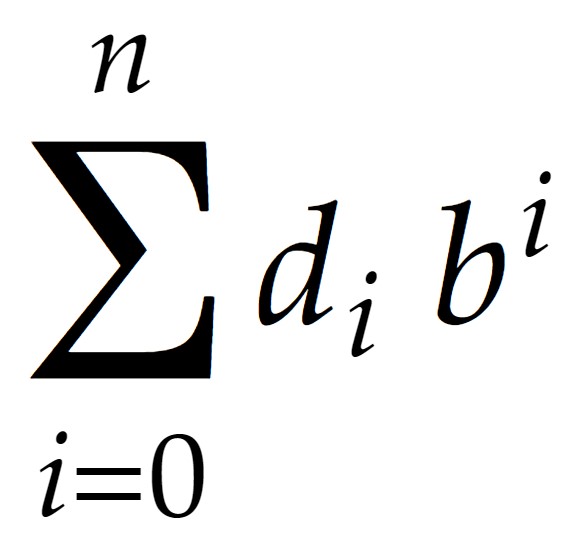
Where d is the digit and b is the numeral system’s base. Other than that we have our index i starting at zero so that we start with the base’s 0th power as demonstrated before. Let’s make use of this formula one last time on a decimal string of digits before we take a look at binary. We will start with the string of digits 65204:
d=4 | 4 * 10^0 =
b=10 | 4 * 1 =
i=0 | 4
d=0 | 0 * 10^1 =
b=10 | 0 * 10 =
i=1 | 0
d=2 | 2 * 10^2 =
b=10 | 2 * 100 =
i=2 | 200
d=5 | 5 * 10^3 =
b=10 | 5 * 1000 =
i=3 | 5000
d=6 | 6 * 10^4 =
b=10 | 6 * 10000 =
i=4 | 60000
Four ones, zero tens, two one-hundreds, five one-thousands, and six ten-thousands:
4 + 0 + 200 + 5000 + 60000 =
65204
Binary | Base 2
Binary, just like decimal, is a positional numeral system, and we can work out what the value of a binary string is using the same method and formula. The only difference between binary and decimal is that binary uses just two unique symbols. In the following examples we’ll be using the first two digits of the decimal system we’re so used to: 0, and 1. In the binary world, we’ll refer to these as bits instead of digits (binary digits!). We could choose to use any two unique symbols such as 🐄 and 🐖, but since we are so familiar with these bits which conveniently represent the same cardinality within the decimal system we will use these. As there are only two unique symbols for us to use here binary is also known as base 2.
Let’s look at a binary string of bits: 110101. You’ll notice that if we’re not careful we could consider this to be a perfectly inconspicuous decimal number: one-hundred-and-ten-thousand-one-hundred-and-one. It could well be one, but we are working within the binary numeral system, now, and so when we apply our formula this time around, the answer should be a little more interesting and less obvious. Again, as with all of our examples, we’ll start with the least-significant bit.
d=1 | 1 * 2^0 =
b=2 | 1 * 1 =
i=0 | 1
d=0 | 0 * 2^1 =
b=2 | 0 * 2 =
i=1 | 0
d=1 | 1 * 2^2 =
b=2 | 1 * 4 =
i=2 | 4
d=0 | 0 * 2^3 =
b=2 | 0 * 8 =
i=3 | 0
d=1 | 1 * 2^4 =
b=2 | 1 * 16 =
i=4 | 1
d=1 | 1 * 2^5 =
b=2 | 1 * 32 =
i=5 | 32
One ones, zero twos, one fours, zero eights, one sixteens, and one thirty-twos.
1 + 0 + 4 + 0 + 16 + 32 = 53
And with that, rather trivially, we find that 110101 in binary is 53 in decimal! The step-by-step process is extremely similar to when we stepped through decimal strings of digits. The only difference is that we are now working in base 2 and so we see a different pattern emerge.
4 * 1 | 1 * 1
0 * 10 | 0 * 2
2 * 100 | 1 * 4
5 * 1000 | 0 * 8
6 * 10000 | 1 * 16
0 * 100000 | 1 * 32
On the left we have our decimal number, and we can see as the digits become more significant we multiply by ten every time. On the right we have our binary number and instead of multiplying by ten every time we simply multiply by our base: two.